En
期刊文章
文章精选
当期目录
过刊浏览
高被引
高下载
特邀文章
专刊合集
待刊文章
Volume 107
您当前的位置：首页 > 期刊文章 > 当期目录 > Volume 107
Characteristics of mass transfer between bubble and emulsion phases of high-temperature gas–solid bubbling fluidized beds
Jinchao Xie a, Han Gao b, Qingjin Zhang b, Jinliang Chen a, Zezhong Wang a, Chenxi Zhang a c *, Dingrong Bai a b *
a Ordos Laboratory, Ordos, Inner Mongolia, 017010, China
b Key Laboratory on Resources Chemicals and Material of Ministry of Education, Shenyang University of Chemical Technology, Shenyang, 110142, China
c Beijing Key Laboratory of Green Chemical Reaction Engineering and Technology, Department of Chemical Engineering, Tsinghua University, Beijing, 100084, China
10.1016/j.partic.2025.09.014
Volume 107, December 2025, Pages 26-34
Received 10 August 2025, Revised 18 September 2025, Accepted 20 September 2025, Available online 25 September 2025, Version of Record 3 October 2025.
E-mail: cxzhang@mail.tsinghua.edu.cn; baidingrong@ordoslab.cn
Highlights

• The two-phase model can quantify mass transfer coefficients (K) from gas residence time distributions.

• The K peaks between 300 and 800 °C and stabilizes above 1200 °C.

• Mass transfer flux between the two phases reduces with superficial gas velocity.

• Static bed height and particle size affect the variation of K with temperature.


Abstract

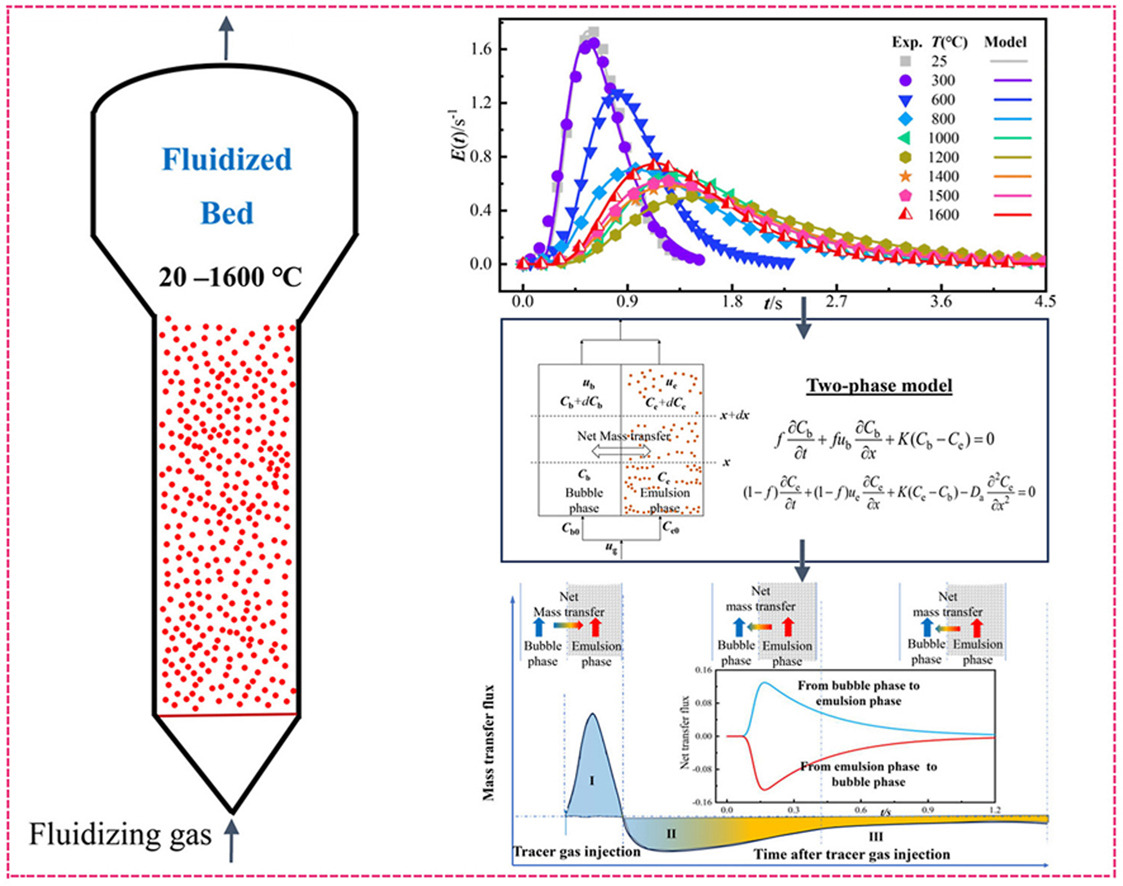
Understanding interphase mass transfer is crucial for the efficient design and operation of gas–solid fluidized beds, which are widely used in various industrial processes. However, research on mass transfer behavior in such systems, particularly at high temperatures (e.g., >1000 °C), remains sparse. This study, dedicated to Profs. Yong Jin and Zhiqing Yu's contributions to fluidization, elucidates the mass transfer behavior of gas-solid bubbling fluidized beds at temperatures up to 1600 °C by modeling gas residence time distribution data using a two-phase model. We examine the effects of temperature, gas velocity, bed height, and particle size on mass transfer characteristics. The results reveal that the mass transfer flux increases with temperature up to 800 °C, peaking within this range before stabilizing above 1200 °C. This trend is closely linked to the behavior of bubble dynamics, where bubble size initially decreases significantly as temperature rises, eventually reaching a plateau at higher temperatures. Experimental pressure fluctuation analysis validates this behavior, further supporting the observed temperature effects on bubble dynamics. Higher gas velocity reduces the mass transfer flux and mitigates back-mixing, while bed height and particle size affect bubble dynamics in a nonlinear manner. Experimental validation confirms the potential of these findings for optimizing the design and operation of high-temperature bubbling fluidized bed reactors.

Graphical abstract
Keywords
High-temperature fluidized bed; Mass transfer coefficient; Gas residence time distribution; Two-phase model; Bubble size
文章导读