En
期刊文章
文章精选
当期目录
过刊浏览
高被引
高下载
特邀文章
专刊合集
待刊文章
Volume 107
您当前的位置：首页 > 期刊文章 > 当期目录 > Volume 107
Modeling erosion in dense liquid-solid jet: A comparative study of particle interaction effects using DDPM and DPM
Xuewen Cao a b *, Haoxuan Qu a, Zhongying Xu a, Haopeng Zhang a, Zeyu Zhang a, Wenshan Peng b *, Jiang Bian c
a College of Pipeline and Civil Engineering, China University of Petroleum (East China), Qingdao, 266580, China
b National Key Laboratory of Marine Corrosion and Protection, Luoyang Ship Material Research Institute, Qingdao, 266237, China
c School of Petroleum Engineering, Yangtze University, Wuhan, 430100, China
10.1016/j.partic.2025.10.015
Volume 107, December 2025, Pages 274-286
Received 2 September 2025, Revised 11 October 2025, Accepted 20 October 2025, Available online 30 October 2025, Version of Record 10 November 2025.
E-mail: caoxw@upc.edu.cn; pengwenshan1386@126.com
Highlights

• A new erosion rate prediction method considers particle interactions under high concentration conditions.

• DDPM model reveals particle interactions reduce erosion rates.

• The erosion rate increases with flow rate and particle size.


Abstract

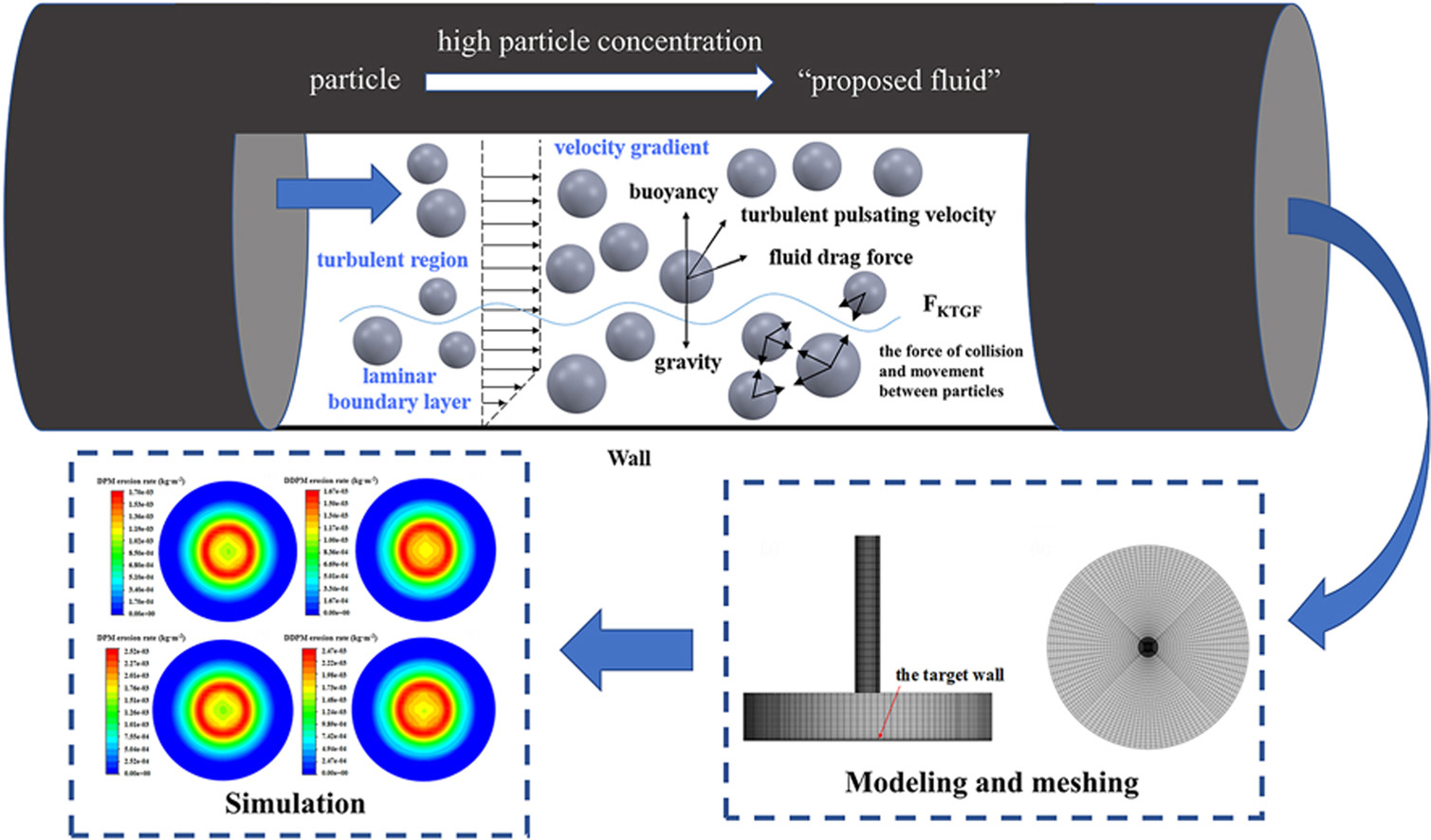
Operational reliability of shale gas pipelines is critically compromised by solid particle erosion, and the effect of particle interactions on the erosion mechanism under high concentration conditions has not been fully investigated. In this study, a numerical model of liquid-solid direct jet erosion considering particle interactions is established, and the fluid flow characteristics, particle trajectories and erosion damage patterns are analyzed by comparing the discrete phase model (DPM) with the dense discrete phase model (DDPM). A systematic investigation into the influence of particle concentration, flow velocity and particle size on erosion mechanisms was conducted employing the Realizable k-ε turbulence model, the Zhang erosion model, and an experimentally verified computational mesh. The results show that increased particle concentrations lead to lower erosion rates, and DDPM predictions are about 2.5 % lower than those of two-way DPM, which overestimates erosion by ignoring particle-fluid interactions. DDPM is more effective at high concentrations, and the distribution of particle collision velocities it captures shows that particle collision velocities are greater in the center region, but DDPM predicts higher values at the radial peak, leading to an overestimation in the severely eroded zone. This study develops a more accurate numerical modeling approach for predicting erosion in high concentration liquid-solid two-phase jets.

Graphical abstract
Keywords
Particle interactions; Numerical simulation; Jet; Multiphase flow
文章导读