En
期刊文章
文章精选
当期目录
过刊浏览
高被引
高下载
特邀文章
专刊合集
待刊文章
Volume 107
您当前的位置：首页 > 期刊文章 > 当期目录 > Volume 107
Residence time distribution of powders in a vertical single screw reactor: Experiments using salt-coated tracer particles and simulations
R. Sriram Rajendra a b, Anil V. Palgadhmal a, Amol A. Kulkarni a b *
a Chemical Engineering & Process Development Division, CSIR-National Chemical Laboratory, Dr. Homi Bhabha Road, Pune, 411008, India
b Academy of Scientific and Innovative Research (AcSIR), Sector 19, Kamla Nehru Nagar, Ghaziabad, 201002, Uttar Pradesh, India
10.1016/j.partic.2025.10.008
Volume 107, December 2025, Pages 313-326
Received 16 April 2025, Revised 28 September 2025, Accepted 8 October 2025, Available online 24 October 2025, Version of Record 11 November 2025.
E-mail: aa.kulkarni.ncl@csir.res.in
Highlights

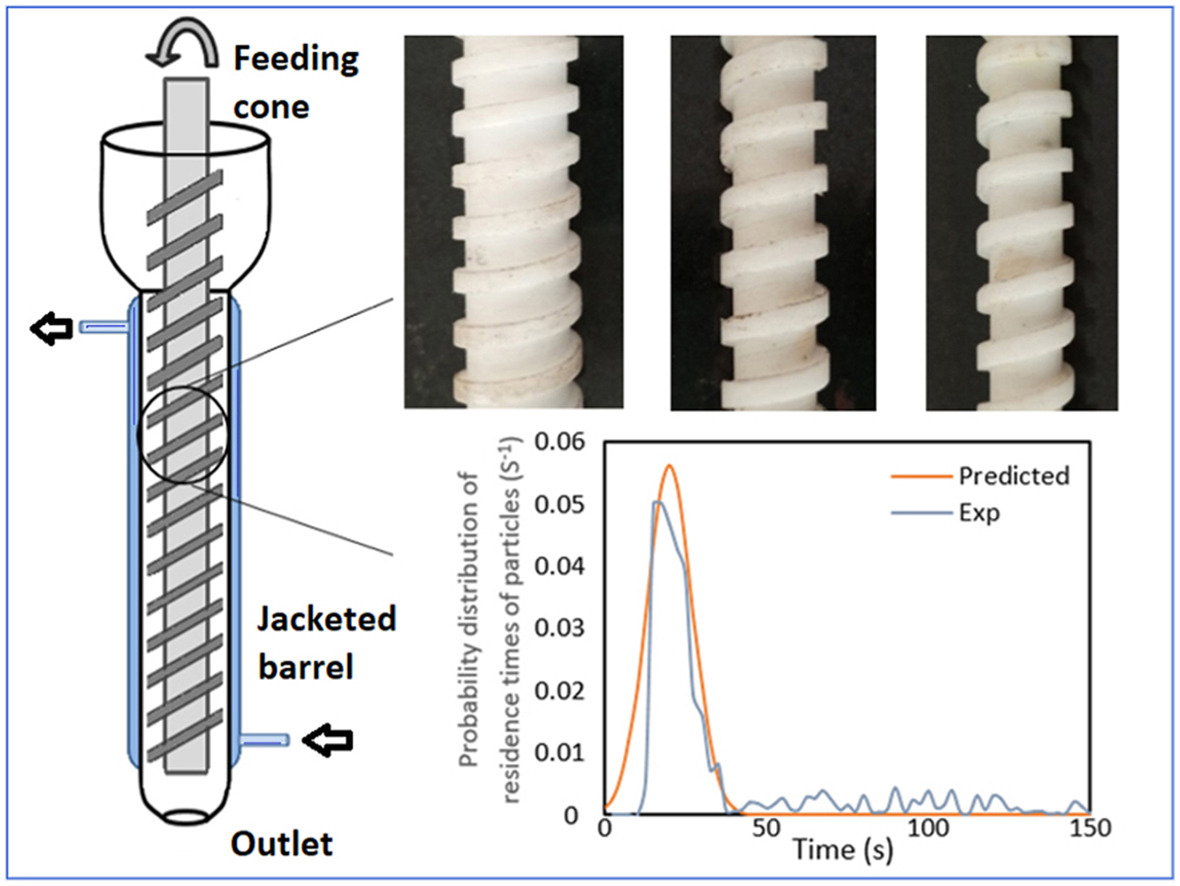
• Residence time distribution for powders is reported in a vertical single screw reactor.

• Experiments were conducted using different screws with particles of 25 < dp < 50 μm.

• Dispersion coefficient was estimated using true and bulk densities of the powder and shear rate.

• A novel method has been developed for measurement of RTD in powder flows.

• A screw can act as a PFR when its diameter is large with lower depth and helix angle.


Abstract

The use of single and twin-screw extruders for solid-phase reactions is a promising method to intensify a process in a more sustainable manner. In this manuscript, we report a detailed analysis of the residence time distribution (RTD) in vertical single-screw reactors. The results will help in the selection of the right screw design that would help achieve the desired residence time, which is necessary for a reaction to happen. Experiments were conducted in three vertical screw reactors (having fixed shaft diameter) with varying dimensions using granular free-flowing powders of sodium chloride and silica with a mean particle size of ∼25μm. RTD behavior was modeled using the radial particle velocities in the screw reactor's centrifugal field. Further, a method is proposed for estimating the axial dispersion coefficient of dry powders in such sheared flows using true and bulk densities of the powder and the screw shear rate. This dispersion coefficient is used in the axially dispersed plug flow model to describe the RTD behavior of screw reactors with acceptable accuracy. The theoretically predicted and experimentally obtained dispersion coefficients are found to be similar thereby confirming the suitability of the model.



Graphical abstract
Keywords
文章导读