Improved drag force calculation in CFD-DEM using coarse cell for dilute large-sized particles: Effective projected area for drag force distribution--颗粒学报PARTICUOLOGY

Zhang, S., Gui, N., Luo, Y., Yang, X., & Jiang, S. (2025). Improved drag force calculation in CFD-DEM using coarse cell for dilute large-sized particles: Effective projected area for drag force distribution. Particuology, 105, 340-356. https://doi.org/10.1016/j.partic.2025.08.013

Improved drag force calculation in CFD-DEM using coarse cell for dilute large-sized particles: Effective projected area for drag force distribution

Shen Zhang, Nan Gui^*, Yiyang Luo, Xingtuan Yang, Shengyao Jiang^*

Institute of Nuclear and New Energy Technology, Collaborative Innovation Center of Advanced Nuclear Energy Technology, Key Laboratory of Advanced Reactor Engineering and Safety, Ministry of Education, Tsinghua University, Beijing, 100084, China

10.1016/j.partic.2025.08.013

Volume 105, October 2025, Pages 340-356

Received 21 June 2025, Revised 4 August 2025, Accepted 15 August 2025, Available online 29 August 2025, Version of Record 4 September 2025.

E-mail: guinan@mail.tsinghua.edu.cn

Highlights

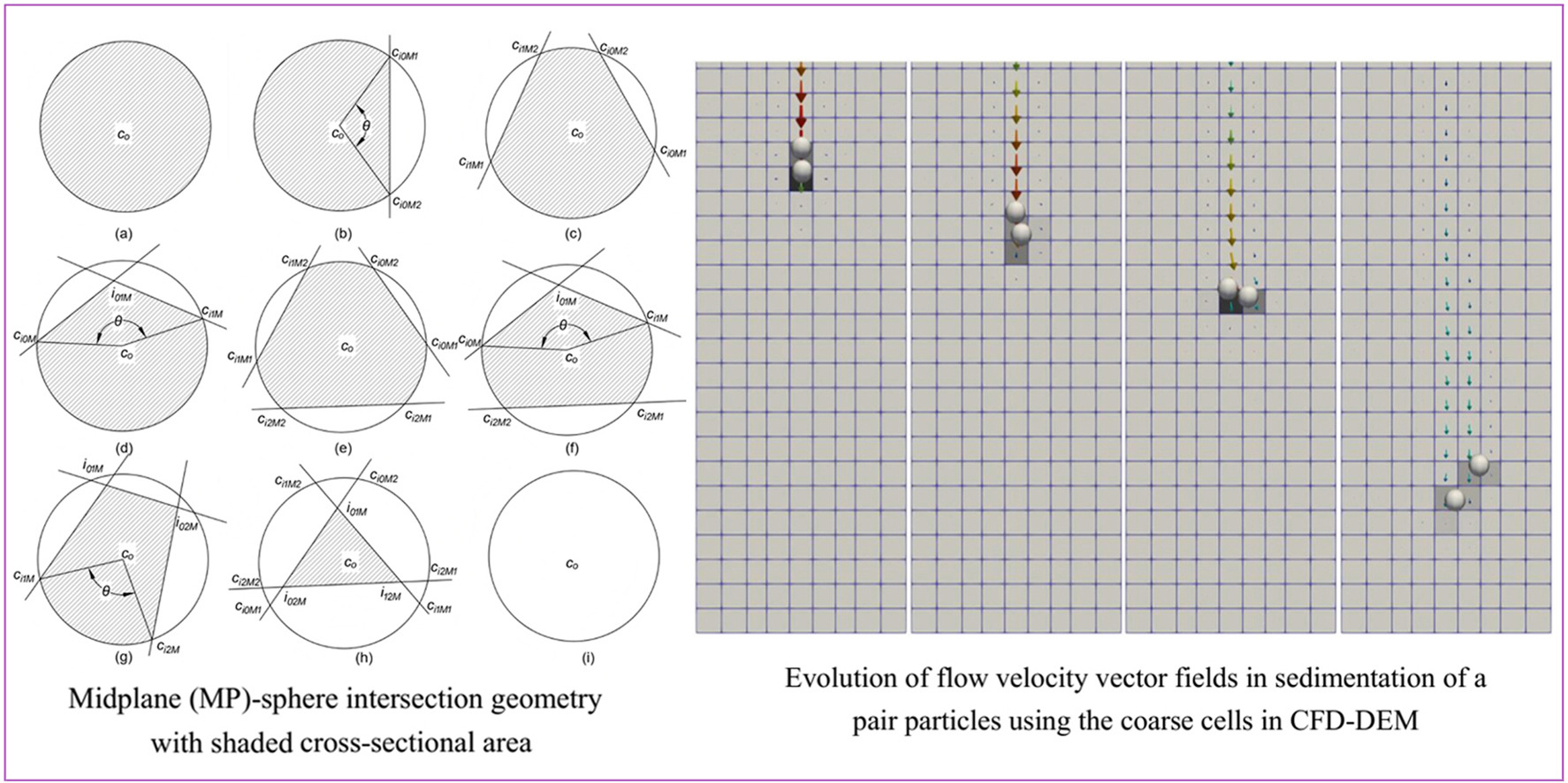
• An effective projected area (EPA) based analytical solution is implemented to eliminate abrupt drag variations.

• Particle-grid position classification system established and statistically validated.

• Combined face-wind and EPA classification achieves accurate particle-cell modeling.

• The continuous EPA evolution resolves traditional PCM's drag discontinuities.

• Model validated through demonstrated smoother and physically consistent transitions.

Abstract

This study addresses a critical challenge in CFD-DEM simulations: the accurate assignment of drag force to fluid mesh cells when the cell size exceeds particle sizes. Traditional particle centroid method (PCM) approaches often lead to abrupt drag force variations as particles cross cell boundaries due to their discrete nature. To overcome this limitation, we propose a novel algorithm that computes an analytical solution for the effective projected area (EPA) of particles within computational cells, aligned with the relative velocity direction. The drag force is then proportionally scaled according to this EPA calculation. The paper presents a specific implementation case of our algorithm, focusing on scenarios where a cell vertex resides within a particle boundary. For EPA determination, we introduce an innovative classification approach based on face-windward surface relations. Extensive validation involved 100,000 test cases with varying cell-particle relative positions (all constrained by the vertex-in-particle condition), systematically classified into 18 types using our scheme. Results demonstrate that all computed EPA values remain within theoretical bounds, confirming the classification's comprehensiveness. Through 5 classic particle movement simulations, we show that our method maintains continuous EPA variation across time steps - a marked improvement over PCM's characteristic discontinuities. Implementation within the CFD-DEM framework for single-particle sedimentation yields terminal velocities that closely match experimental data while ensuring smooth drag force transitions between fluid cells. Compared to PCM, the present method reduces the relative error in terminal settling velocity by approximately 43 %. Moreover, comparative studies of dual-particle sedimentation demonstrate our algorithm's superior performance relative to conventional PCM approaches. For Particle 1, the terminal vertical velocity predicted by the present method reduces the relative error by approximately 17 % compared to PCM. These advances significantly enhance simulation fidelity for particle-fluid interaction problems where cell-particle size ratios challenge traditional methods.

Graphical abstract

Keywords

Gas-particle; Drag force; Computational fluid dynamics discrete-element method; Face-windward surface relation; Effective projection area; Volume in mesh

文章导读