En
期刊文章
文章精选
当期目录
过刊浏览
高被引
高下载
特邀文章
专刊合集
待刊文章
Volume 108
您当前的位置：首页 > 期刊文章 > 过刊浏览 > Volumes 108-119 (2025) > Volume 108
Kianimoqadam, A., & Lapp, J. (2026). Gaussian integral method for void fraction. Particuology, 108, 125-142. https://doi.org/10.1016/j.partic.2025.10.014
Gaussian integral method for void fraction
Alireza Kianimoqadam, Justin Lapp *
Department of Mechanical Engineering, University of Maine, Orono, ME, 04469, USA
10.1016/j.partic.2025.10.014
Volume 108, January 2026, Pages 125-142
Received 20 July 2025, Revised 16 October 2025, Accepted 20 October 2025, Available online 1 November 2025, Version of Record 3 December 2025.
E-mail: Justin.Lapp@Maine.edu
Highlights

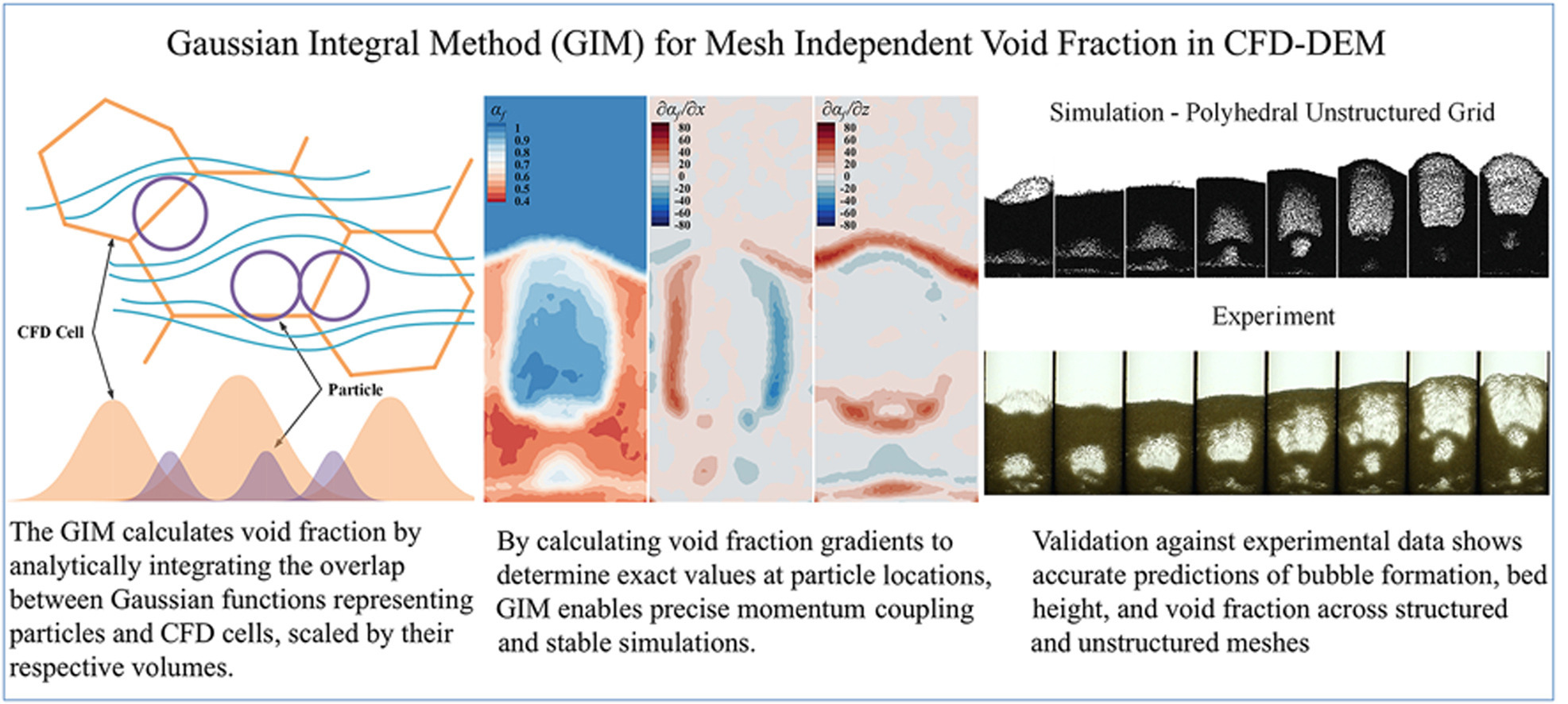
• Gaussian Integral Method is introduced for computing void fractions.

• The method applies to CFD-DEM simulations with a variety of CFD cell types.

• The method smooths void fraction gradients for more stable simulations.

• Accuracy in the fluid-particle interaction is retained by tuning coefficients.


Abstract

A novel method, the Gaussian Integral Method (GIM), is presented for calculating void fractions in Computational Fluid Dynamics–Discrete Element Method (CFD-DEM) simulations. GIM is versatile and applicable to various grid types, including structured and unstructured polyhedral meshes, without requiring special boundary treatments. An optimization technique is introduced to make GIM independent of grid resolution and type. The method is validated against experimental data from a fluidized bed, demonstrating that GIM produces realistic simulations closely resembling experimental observations. Additionally, unstructured polyhedral grids using GIM outperform structured grids of equivalent resolution, yielding results more aligned with experimental data. The gradient of the void fraction is computed in the CFD solver and utilized in the DEM solver for precise estimation at particle locations. Overall, GIM provides an effective solution for void fraction calculations in particulate media simulations with complex geometries, enhancing the accuracy and applicability of CFD-DEM simulations for industrial processes.

Graphical abstract
Keywords
Void fraction; Volume fraction; Discrete element method; CFD-DEM; Gaussian method
文章导读