
Improved drag force calculation in CFD-DEM using coarse cell for dilute large-sized particles: Effective projected area for drag force distribution
张申,桂南*,罗一洋,杨星团,姜胜耀
Keywords: Gas-particle; Drag force; Computational Fluid Dynamics Discrete - Element Method; Face-windward surface relation; Effective projection area; Volume in mesh
DOI: 10.1016/j.partic.2025.08.013
本文提出一种适用于流体网格单元大于颗粒尺度的CFD-DEM模拟中高精度曳力分配算法。该方法的特点是,通过解析颗粒相对于流体-颗粒速度的有效投影面积(effective projected are,EPA)且按各相交单元的EPA比例分配曳力。并为网格顶点位于颗粒内部的算例提供了专门的实现方案。由多组颗粒运动模拟的验证结果表明,方法能够实现将分配到流体单元上的曳力随时间平滑变化,彻底消除了传统质心法(particle centroid method,PCM)的不连续性。在单颗粒沉降算例中,终端速度与实验数据高度吻合,实现了颗粒跨越网格时曳力的平滑过渡;在双颗粒沉降算例中,本文提出的方法性能显著,与传统的PCM方法相比,初始位于上方的颗粒其终端竖直速度相对误差降低了近17%。
相关研究成果发表于PARTICUOLOGY(Volume 105),欢迎感兴趣的读者扫描下方二维码或者点击文末“阅读原文”进入ScienceDirect官网阅读、下载!

亮点
- 本文提出一种CFD-DEM模拟中颗粒在流体网格栅元内有效投影面积(EPA)的解析算法,可实现曳力的精确分配;
- 基于FWSR(face-windward surface relations)分类绘制了几何示意图,进一步为提出的方法提供了更直观的理解;
- 方法可有效解决栅元曳力分配随时间突变的问题,实现曳力随时间的平滑连续变化。
研究背景
颗粒及气固多相流广泛存在于化工反应器、流化床和能源系统等工业过程中。在众多的数值模拟方法中,非解析CFD-DEM(计算流体力学-离散元法)因其在计算精度、效率与可扩展性之间的良好平衡,已成为广泛应用的重要工具。然而,作为当前CFD-DEM中常用的曳力分配策略,传统质心法存在明显的局限性,它仅依据粒子质心是否位于某一网格单元内来分配曳力,虽然实现过程比较简单,但在粒子跨越网格边界时会导致受力发生非物理性突变,严重影响计算的连续性和真实性。
为克服这一缺陷,本文提出一种基于面积划分的解析算法,通过精确计算粒子与网格单元相交部分在相对流速方向上的有效投影面积(EPA),以实现在相关单元间按比例合理分配曳力。该方法在保持解析解计算效率的同时,有效确保了粒子跨越网格过程中曳力变化的连续性,同时实现了与流体-粒子相对速度方向一致的物理合理的曳力分布,显著提升了多相流数值模拟的精度与可靠性。
要点精读
稀疏颗粒流中,作用在颗粒上的曳力可表示为:
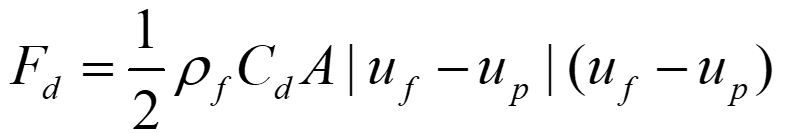 (1)
(1)
根据曳力公式,若能准确确定EPA(即颗粒迎风面在某一网格单元内部分沿颗粒与流体相对速度方向的投影面积),便可直接计算该网格单元所分配的曳力。因此,EPA的精确度对于曳力在计算网格中的准确空间分布至关重要。
如图1(a)所示,球形颗粒与三个蓝色网格面片i0、i1和i2相交,且由三个面片构成的顶点位于颗粒内部;蓝色箭头表示颗粒与流体的相对速度方向;垂直于该方向并通过球心的平面称为MP平面;EPA对应于图1(b)中黑色阴影区域沿相对速度方向的投影面积。
一种直接的计算思路是,先求该曲面区域的表面积,再将其投影至相对速度方向。但该方法需对曲面进行积分,解析过程复杂且计算成本较高。
另一种更高效的策略是,该黑色阴影区域沿速度方向的投影面积,在数学上可等价于四个平面(即,i0、i1、i2和MP平面)上各自有效区域沿同一方向投影面积的代数和,如公式(2)所示,其中,平面i0、i1和 i2上的有效区域对应于图1(b)中的蓝色阴影部分。通过这一转换,将原本复杂的曲面积分问题转化为多个可解析求解的平面投影面积之和,从而在确保精度的同时显著降低了计算的复杂度。
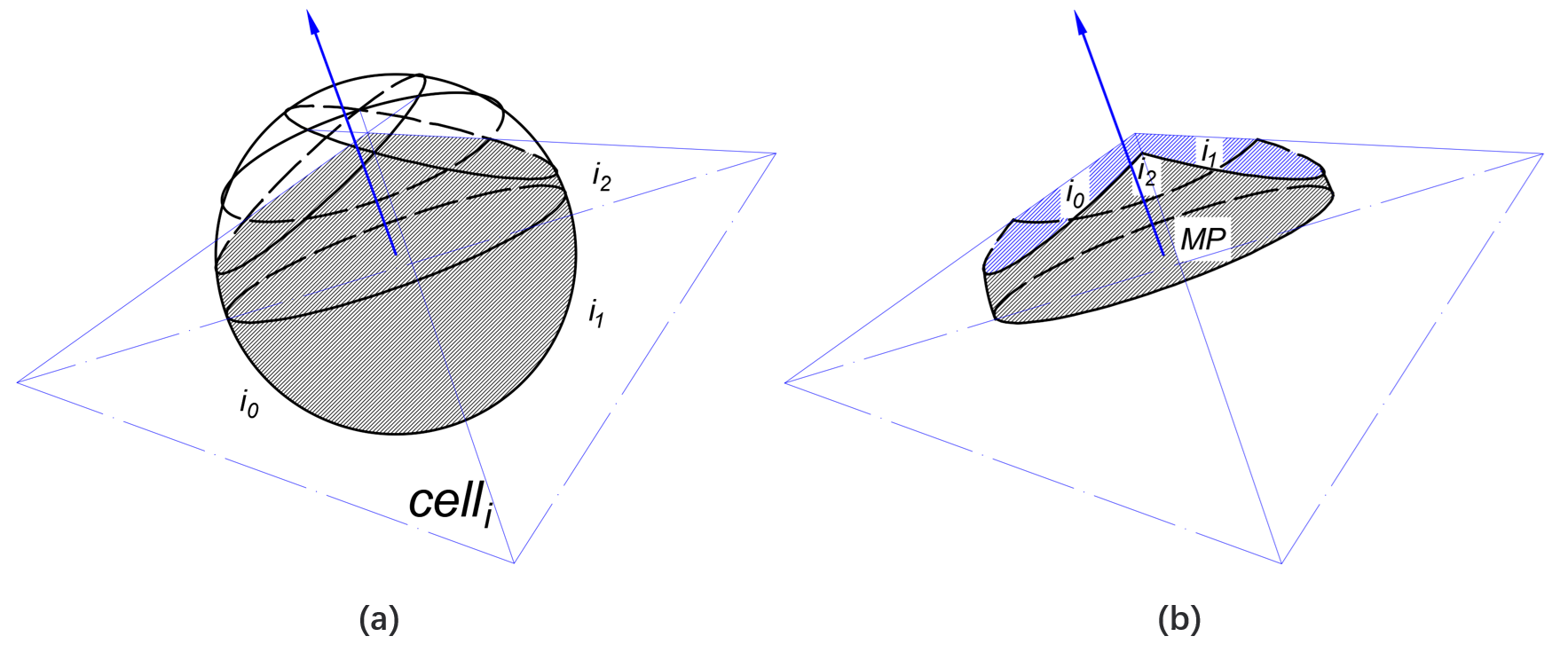
图1. 有效投影面积的示意图(a) 部分位于网格栅元内的球形颗粒;(b) 位于网格栅元内的颗粒正半球部分
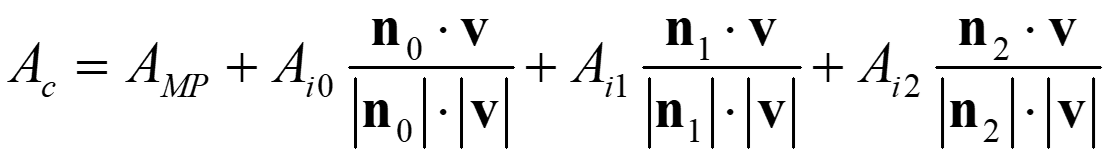 (2)
(2)
以上述高效策略为主要思路,并以最具代表性的情形(图1a)为例进行分析,该情形中颗粒同时与某一网格栅元的三个面片及三条棱相交,且栅元的一个顶点位于颗粒内部。
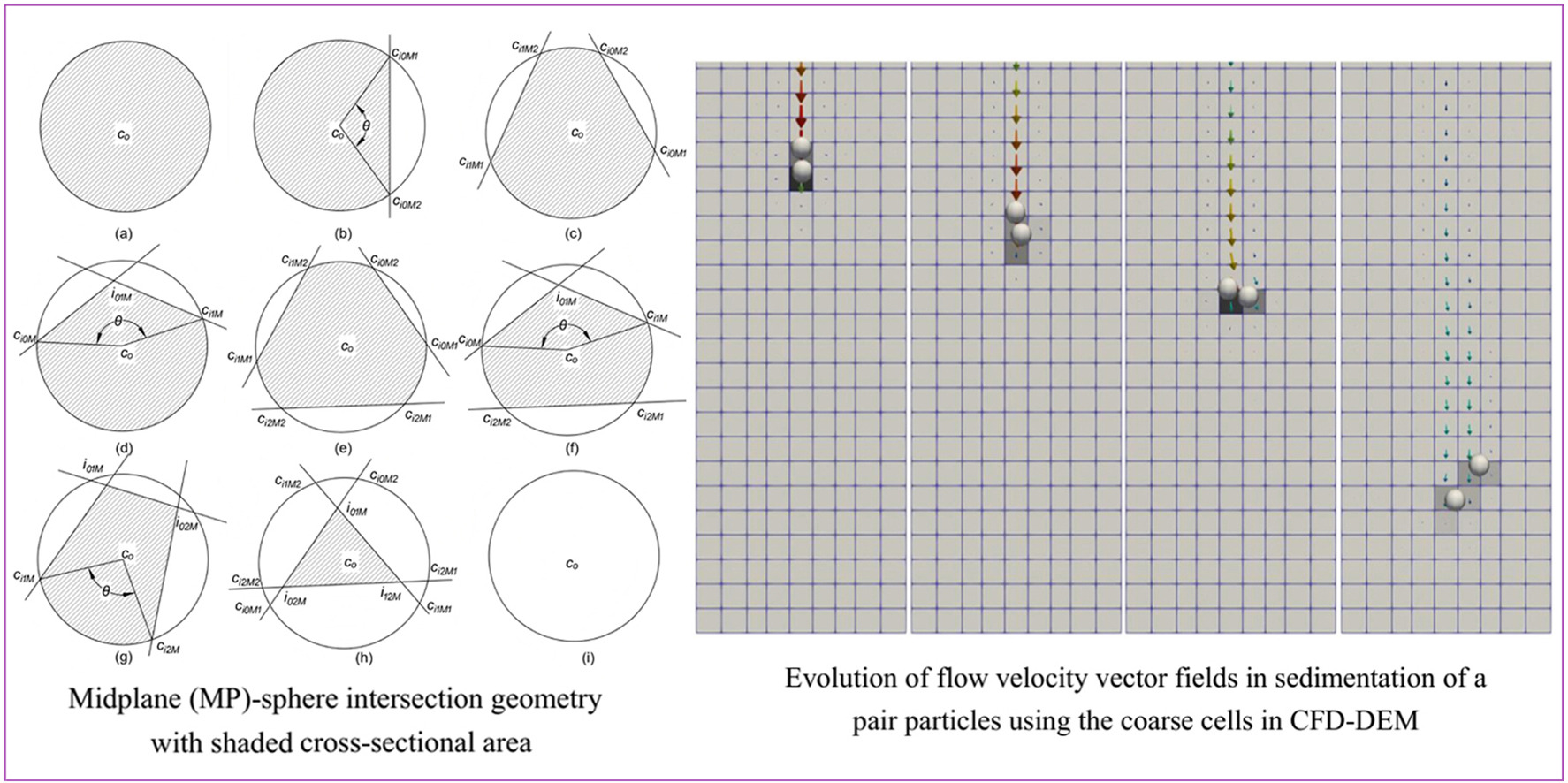
计算颗粒在网格栅元内的EPA时,关键在于判断网格栅元的面片是否与颗粒迎风面相交,这一判断直接决定了迎风面在栅元内部投影面积的计算方法。因此,本文以与迎风面相交的面片数目作为首要分类依据,并基于此原则,将各种情形系统归纳为18种类别,如图2所示。
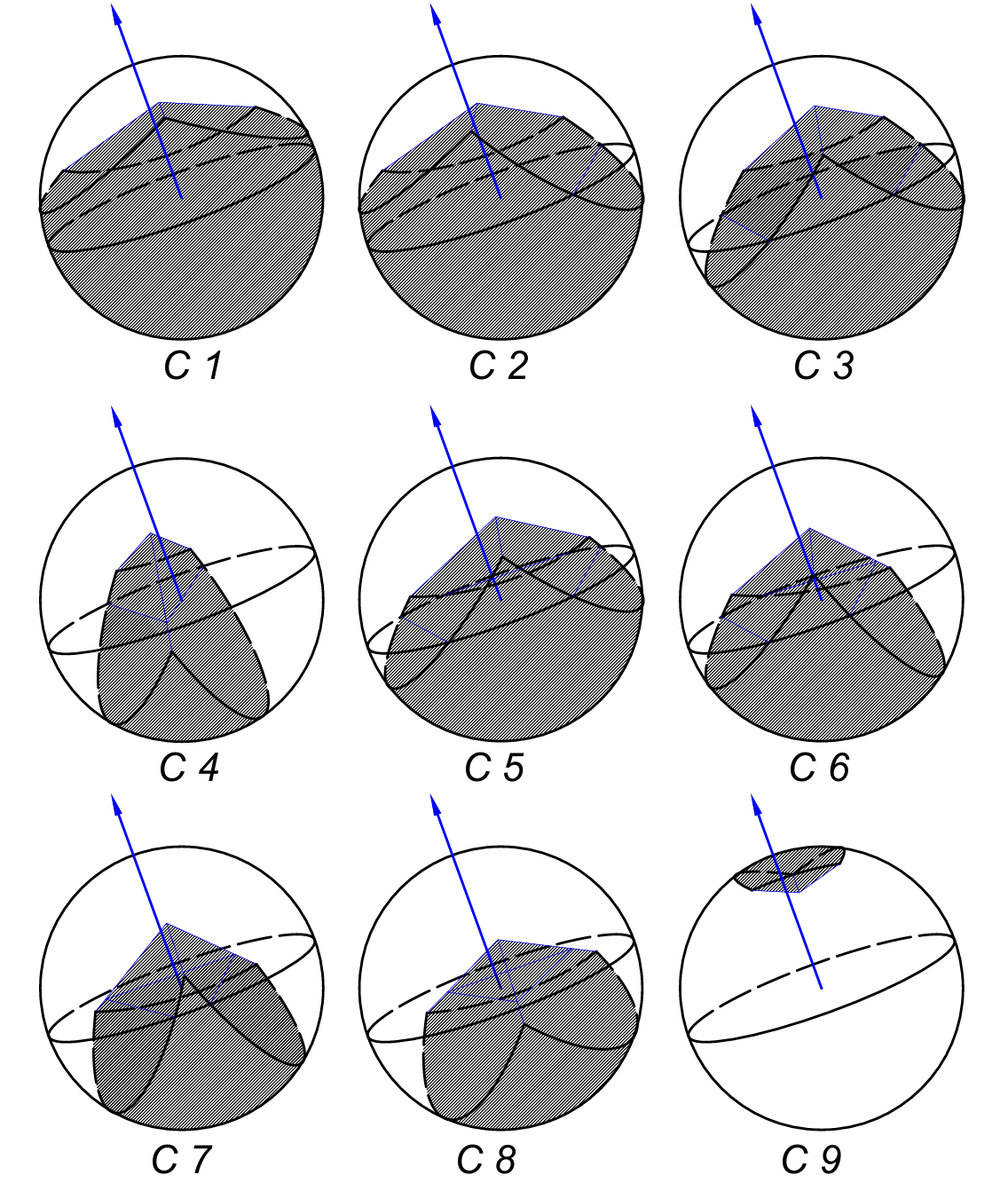
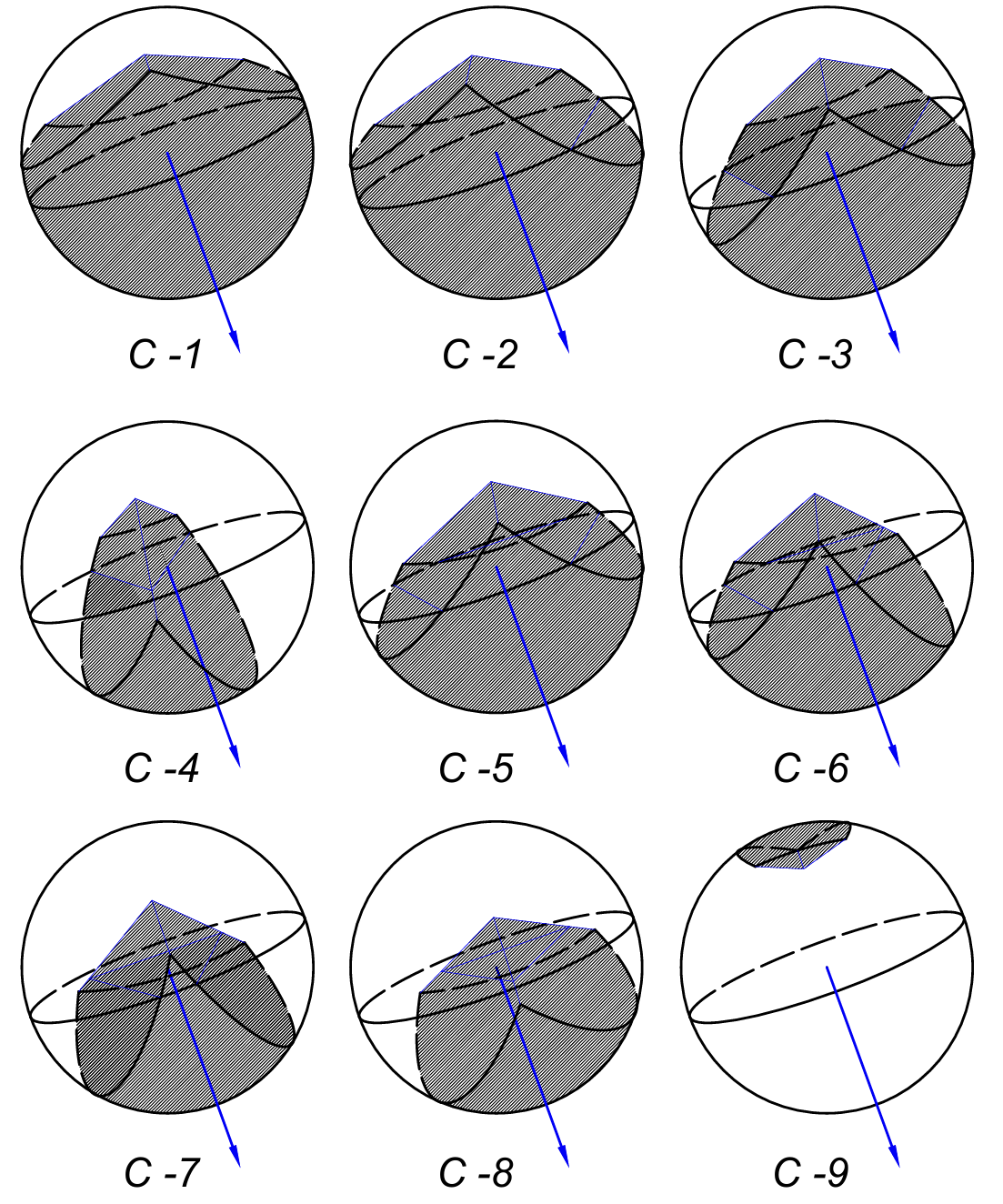
图2. 网格栅元面与球形颗粒迎风面相交关系分类
一旦确定具体情形所属类别,便可根据表1与图3提供的参数代入公式(2)直接计算颗粒在此网格栅元的有效投影面积(Ac)。
这一系统化方法不仅适用于所有可能的颗粒-网格栅元相交情形,而且能够准确确定EPA,因此,可在CFD-DEM耦合模拟中实现精确的曳力分配。
表1. 基于面元–迎风面分类体系的不同类别公式组合
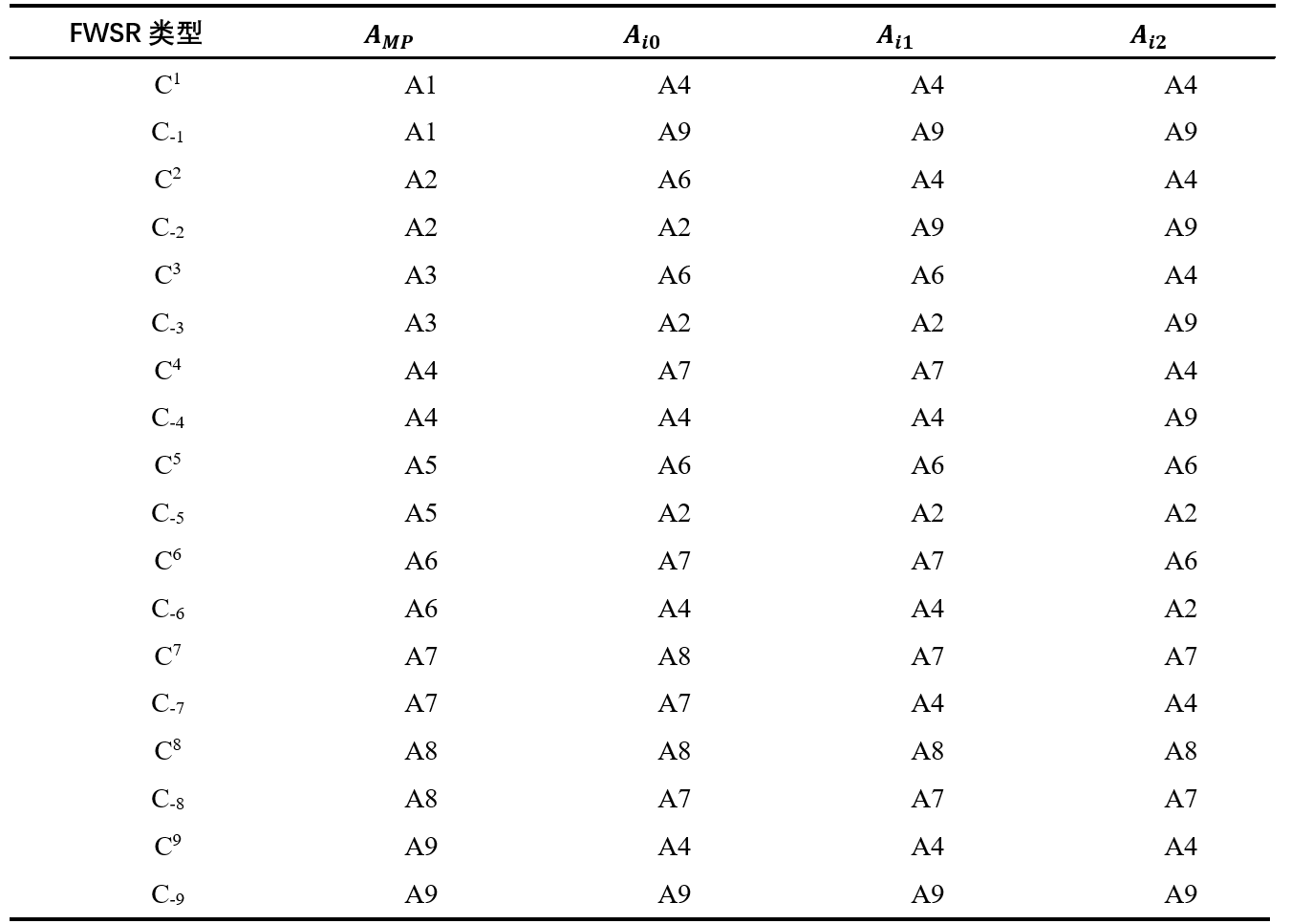
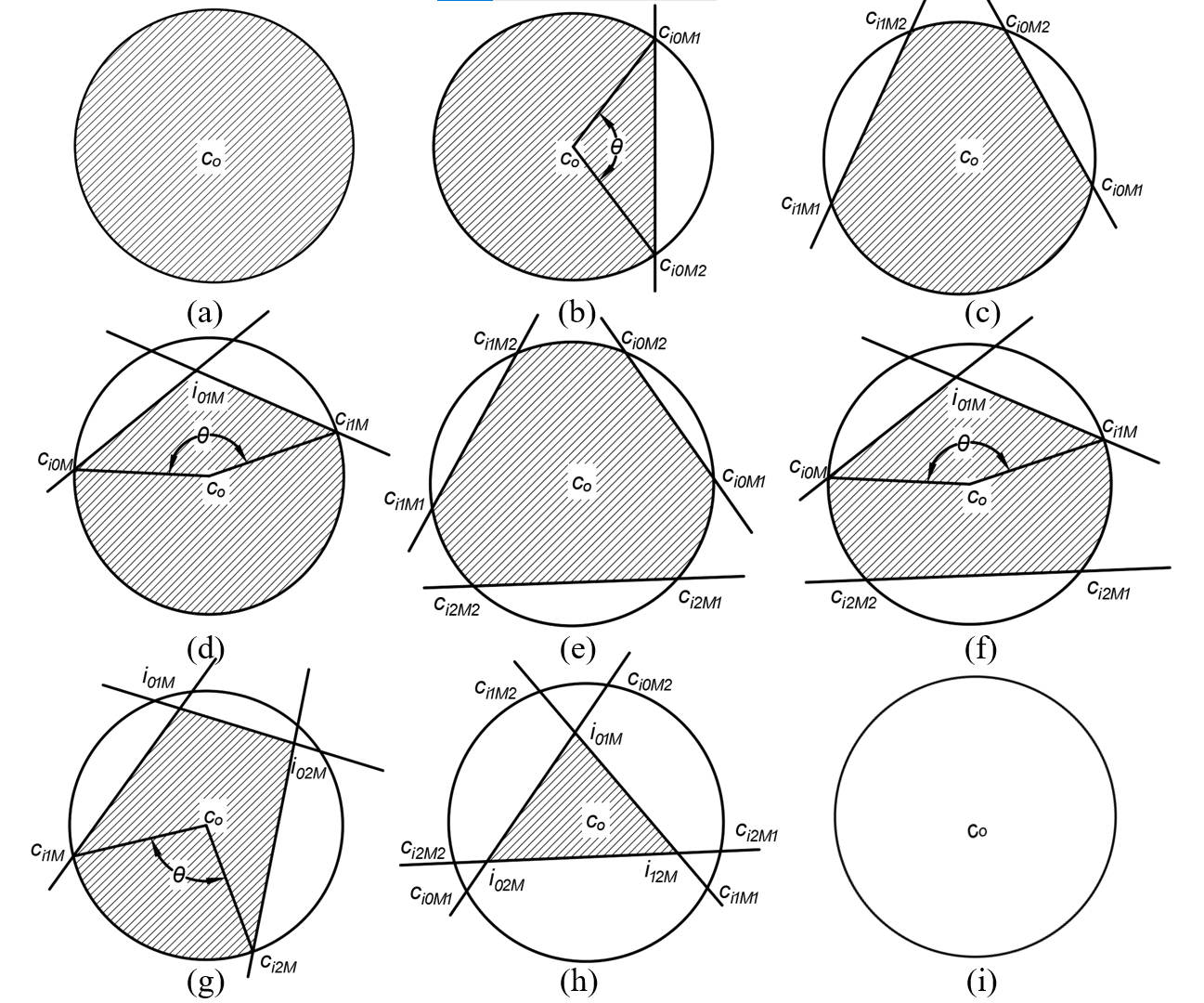
图3. 截面类型分类(a),(b),(c),(d),(e),(f),(g),(h),(i)分别对应截面类型A1,A2,A3,A4,A5,A6,A7,A8,A9
在获得Ac后,即可根据公式(3)进一步求得颗粒分配至该栅元的曳力。
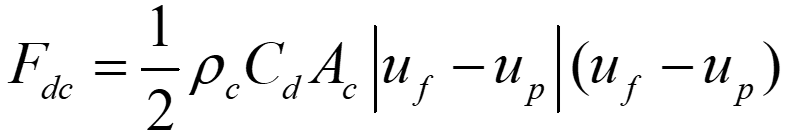 (3)
(3)
结论与展望
本文通过105个随机算例,从统计学角度验证了所提分类方法的完备性与可行性,常见情形(如C9、C4等)出现频率较高,罕见情形(如C-5、C1等)频率较低,且有效投影面积(EPA)频率分布符合完备性要求。颗粒运动算例表明,本文提出的方法实现了EPA随时间的连续变化,避免了传统质心法(PCM)的阶跃突变,为连续曳力分配提供了基础。在单/双颗粒沉降的CFD-DEM模拟中,呈现出更高的精度,实现了多栅元间更合理、平滑的曳力分布,符合物理规律。未来将拓展该算法至更多CFD-DEM应用场景,并深入研究其对流场计算的影响。
作者简介

张申,清华大学核研院博士研究生,主要研究方向为CFD-DEM数值模拟。共发表论文9篇。

桂南,清华大学核研院长聘副教授,107室主任,主要从事球床式高温气冷堆堆芯球床流动、两相流动传热、颗粒流及多物理耦合研究。现任中国颗粒学会青年理事,颗粒计算专委会委员,中国能源学会核能组委员,国际先进材料协会会士,“实验与计算多相流(英文刊)”副主编。先后获国际先进材料协会科学家奖、中国颗粒学会青年颗粒学奖。出版英文学术专著2部,发表SCI期刊论文160余篇。
罗一洋,清华大学核研院博士研究生,主要研究方向为太阳能利用、原油管道输运模拟与优化、高温气冷堆堆芯流动与传热,共发表SCI论文10篇。
杨星团,清华大学核能与新能源技术研究院教授、副院长,主要从事先进反应堆工程与安全、热工水力学等领域研究。
姜胜耀,清华大学长聘教授,国家杰出青年基金获得者。历任清华大学人事处处长、副校长、校党委常委、校党委常务副书记等职务。
供稿:原文作者排版:《颗粒学报》编辑部
文章信息
Zhang, S., Gui, N., Luo, Y., Yang, X., & Jiang, S. (2025). Improved drag force calculation in CFD-DEM using coarse cell for dilute large-sized particles: Effective projected area for drag force distribution. Particuology, 105, 340-356. https://doi.org/10.1016/j.partic.2025.08.013.
